题目内容
如图,已知四棱锥 的底面为菱形,且
的底面为菱形,且 ,
,
 ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.

解:(1)如图所示,取AB中点E,连PE、CE.
则PE是等腰△PAB的底边上的中线,所以PE⊥AB.
PE=1,CE= ,PC=2,即
,PC=2,即 .
.
由勾股定理可得,PE⊥CE.又因为ABÌ平面ABCD,CEÌ平面ABCD,
且AB∩CE=E,所以PE⊥平面ABCD.
而PEÌ平面PAB,所以平面PAB⊥平面ABCD.
 (2)(方法1)如图1,在Rt△PEC中,过点E作EF⊥PC于点F,连AF.过A作平面PCD的垂线,垂足为H,连FH.
(2)(方法1)如图1,在Rt△PEC中,过点E作EF⊥PC于点F,连AF.过A作平面PCD的垂线,垂足为H,连FH.
因为AE⊥EC,AE⊥PE,所以AE⊥平面PEC,于是AE⊥PC.
又EF⊥PC,所以PC⊥平面AEF,故PC⊥AF.
已有PC⊥AH,可得PC⊥平面AFH,所以PC⊥FH.
故∠AFH是二面角A-PC-D的平面角.
由AB⊥平面PEC知EF⊥AB,又AB∥CD,所以EF⊥CD.
而已有EF⊥PC,所以EF⊥平面PCD.又因为AH⊥平面PCD,
所以AH∥EF.
由于AB∥平面PCD,所以A、E两点到平面PCD的距离相等,故AH=EF.
所以AEFH是矩形,∠AFH=∠EAF.
在Rt△AEF中,AE=1,EF= ,AF=
,AF= ,所以
,所以 .
.
即二面角A-PC-D的平面角的余弦值是 .
.
(方法2)以AB中点E为坐标原点,EC所在直线为x轴,EB所在直线为y轴,EP所在直线为z轴,建立如图所示的空间直角坐标系.
 则A(0,-1,0),C(
则A(0,-1,0),C( ,0,0),D(
,0,0),D( ,-2,0),P(0,0,1),
,-2,0),P(0,0,1), =(
=( ,1,0),
,1,0), =(
=( ,0,-1),
,0,-1), =(0,2,0).
=(0,2,0).
设 是平面PAC的一个法向量,则
是平面PAC的一个法向量,则 ,即
,即 .
.
取 ,可得
,可得 ,
, .
.
设 是平面PCD的一个法向量,则
是平面PCD的一个法向量,则 ,即
,即 .
.
取 ,可得
,可得 ,
, .
.
故 ,即二面角A-PC-D的平面角的余弦值是
,即二面角A-PC-D的平面角的余弦值是 .
.

 的值域
的值域 ,则
,则 _____________
_____________ ,则判断框中为 ( )
,则判断框中为 ( ) B.
B. C.
C. D.
D.

 五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件
五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件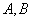 被放在相邻的抽屉内且文件
被放在相邻的抽屉内且文件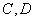 被放在不相邻的抽屉内的概率是 。
被放在不相邻的抽屉内的概率是 。 q D.(
q D.( p)
p) q
q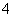 名男生、
名男生、 名女生中选出
名女生中选出 人参加志愿者服务,则至少选出
人参加志愿者服务,则至少选出 A.
A.  B.
B. C.
C.  D.
D.
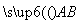 =
= ,
, =
= ,若点D满足
,若点D满足 =2
=2 ,则
,则 =( ).
=( ). 


 和
和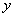 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量 ,对变量
,对变量 ,那么下列说法正确的是( )
,那么下列说法正确的是( ) B.
B.