题目内容
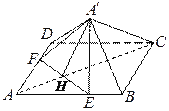
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() 与
与![]() 的交点为
的交点为![]() ,
, ![]() ,现将
,现将![]() 沿线段
沿线段![]() 折起到
折起到![]() 位置,使得
位置,使得![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求五棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在
;(3)存在![]() .
.
【解析】试题分析:(1)要证平面![]() 平面
平面![]() ,即证
,即证![]() 平面
平面![]() ;
;
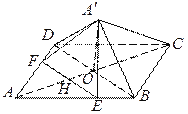
(2) 连接AC,设AC∩EF=H,由已知条件推导出平面A′HC⊥平面ABCD,过点A′作A′O垂直HC且与HC相交于点O,则A′O⊥平面ABCD,由此能求出五棱锥A′-BCDFE的体积.
(3)线段A′C上存在一点M,使得BM∥平面A′EF,A′M=.证明平面MBD∥平面A′EF, ![]() 即可得出结论.
即可得出结论.
试题解析:
(1)由![]() 是正方形,
是正方形, ![]() ,
, ![]() 是
是![]() 的中点,且
的中点,且![]() ,从而有
,从而有![]() 所以
所以![]() 平面
平面![]() , 从而平面,平面
, 从而平面,平面![]() .
.
(2)过点![]() 作
作![]() 垂直
垂直![]() 且与
且与![]() 相交于点
相交于点![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,
,
因为正方形![]() 的边长为
的边长为![]() ,
, ![]() ,得到:
,得到: ![]() ,
,
所以![]() ,所以
,所以![]()
所以五棱锥![]() 的体积
的体积![]() .
.
(3)线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,
, ![]() .
.
证明: ![]()
![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() , 所以平面
, 所以平面![]() 平面
平面![]() ,
,
由![]() 在平面
在平面![]() 内,所以
内,所以![]() 平面
平面![]() .
.

练习册系列答案
相关题目