题目内容
(1)求右焦点坐标是(2,0),且经过点( -2 ,-
)的椭圆的标准方程;
(2)求与椭圆
+
=1有共同的焦点并且与双曲线
-
=1有共同渐近线的双曲线方程.
| 2 |
(2)求与椭圆
| x2 |
| 24 |
| y2 |
| 49 |
| x2 |
| 36 |
| y2 |
| 64 |
(1)由题意,可设椭圆的标准方程为
+
=1,则
∵右焦点坐标是(2,0),经过点( -2 ,-
)
∴c2=a2-b2=4,
+
=1,
解得a2=8,b2=4.
椭圆的标准方程为
+
=1; …(6分)
(2)椭圆
+
=1的焦点坐标为(0,±5),
双曲线
-
=1的渐近线方程为y=±
x,
由题意可设双曲线的标准方程为
-
=1,
则c2=a2+b2=25,
=
,
解得a2=16,b2=9.双曲线的标准方程为
-
=1
| x2 |
| a2 |
| y2 |
| b2 |
∵右焦点坐标是(2,0),经过点( -2 ,-
| 2 |
∴c2=a2-b2=4,
| (-2)2 |
| a2 |
(-
| ||
| b2 |
解得a2=8,b2=4.
椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)椭圆
| x2 |
| 24 |
| y2 |
| 49 |
双曲线
| x2 |
| 36 |
| y2 |
| 64 |
| 4 |
| 3 |
由题意可设双曲线的标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
则c2=a2+b2=25,
| a |
| b |
| 4 |
| 3 |
解得a2=16,b2=9.双曲线的标准方程为
| y2 |
| 16 |
| x2 |
| 9 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1)求右焦点坐标是(2,0),且经过点(-2,-
(1)求右焦点坐标是(2,0),且经过点(-2,- 的椭圆的标准方程;
的椭圆的标准方程; 有共同的焦点并且与双曲线
有共同的焦点并且与双曲线 有共同渐近线的双曲线方程.
有共同渐近线的双曲线方程.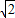 )的椭圆的标准方程.
)的椭圆的标准方程. +
+ =1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.
=1(a>b>0).设斜率为k的直线l交椭圆C于A、B两点,AB的中点为M.证明:当直线l平行移动时,动点M在一条过原点的定直线上.