题目内容
等差数列{an}的公差d∈(0,1),且 ,当n=10时,数列{an}的前n项和Sn取得最小值,则首项a1的取值范围为( )
,当n=10时,数列{an}的前n项和Sn取得最小值,则首项a1的取值范围为( )
|
| A. |
| B. | [ | C. | [﹣ | D. |
|
C解:
 sin(a2+a6)=sin2a4
sin(a2+a6)=sin2a4
于是cos2a6﹣cos2a2=﹣2sin2a4﹣2sin(a6+a2)sin(a6﹣a2)=﹣2sin2a4.sin4d=1,0<d<1.于是d= .
.
因为数列{an}的前10项和S10取得最小值,于是a10≤0且a11≥0a1+9d≤0,且a1+10d≥0得 .故选C.
.故选C.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
设f(x)是定义在R上恒不为0的函数,对任意x,y∈R,都有f(x)•f(y)=f(x+y),若a1= ,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n为常数),则数列{an}的前n项和Sn的取值范围是( )
|
| A. | [ | B. | [ | C. | [ | D. | [ |

 ]
] ]
]
 的最小值是
的最小值是 ; ②已知
; ②已知 则
则 ;
; 在
在 上是增函数;
上是增函数; 则
则 . 其中真命题的是
. 其中真命题的是

 的前
的前 项和为
项和为 且满足
且满足 则
则 中最大的项为 ( )
中最大的项为 ( )







 。下列命题中真命题是 ( )
。下列命题中真命题是 ( ) n∈N*总有
n∈N*总有 ∥
∥ 成立,则数列{an}是等差数列 B.若
成立,则数列{an}是等差数列 B.若 的前
的前 项和为
项和为 ,若点
,若点
 在函数
在函数 的图像上,则
的图像上,则 B、
B、 C、
C、 D、
D、
 中,
中,  ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 ( ) A.4 B.8 C.16 D.36
( ) A.4 B.8 C.16 D.36 是定义在实数集
是定义在实数集 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数 都有
都有 ,则
,则 的值是( )
的值是( ) C.1 D.
C.1 D.
 ,
, 则
则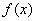 为( )
为( ) 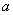 有关
有关