题目内容
已知二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有![]() 成立.
成立.
(1)证明:f(2)=2.
(2)若f(-2)=0,f(x)的表达式.
(3)设g(x)=f(x)-![]() x x∈[0,+∞],若g(x)图上的点都位于直线
x x∈[0,+∞],若g(x)图上的点都位于直线![]() 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
答案:
解析:
解析:
|
解:(1)由条件知 又∵取x=2时, ∴ (2)∵ ∴ 又 ∴ 解出: ∴ (3)由分析条件知道,只要 ∴ 解法2: 即 ①△<0,即[4(1-m)]2-8<0,解得: ② 总之,m∈(-∞,1+ |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
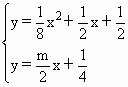 利用相切时△=0,解出
利用相切时△=0,解出 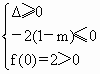 解出:
解出: