题目内容
已知函数f(x)=a(2cos2
+sinx)+b.(Ⅰ)当a=1时，求f(x)的单调递增区间；
(Ⅱ)当a＞0，且x∈[0，π]时，f(x)的值域是[3，4]，求a、b的值.
解：(Ⅰ)∵f(x)=1+cosx+sinx+b=sin(x+
)+b+1,
∴递增区间为[2kπ
,2kπ+
],A∈Z.
(Ⅱ)∵f(x)=a(sinx+cosx)+a+b=
asin(x+
)+a+b,
而x∈[0,π],x+
∈[
,
],sin(x+
)∈[
,1],
故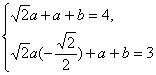
∴
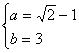
练习册系列答案
相关题目
已知函数f(x)=a-
，若f（x）为奇函数，则a=（ ）
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |