题目内容
已知异面直线a、b所成的角为70°,则过空间任意一点M可作多少条不同的直线与a、b所成的角都是55°.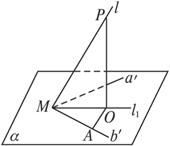
解:过M作a′∥a,b′∥b,分直线与a′、b′共面和异面两种情况讨论.
(1)当所作直线与a′、b′共面时,只有平分110°角的直线l符合题意.
(2)当所作直线l与a′、b′不在同一平面内时(如图),在l上取一点P,作PO⊥α于O,由于PM与a′、b′所成的角相等(55°),因此,P在α上的射影O在70°角的平分线l1上.
∵∠PMA=55°,∠AMO=35°,∠PMO=θ,
则cos55°=cosθ·cos35°.
∴cosθ=
＜1,θ存在且唯一.
同理,相应的与l关于l1对称的直线l′也适合.因此,满足条件的直线有三条.
练习册系列答案
相关题目