题目内容

将函数y=sin(2x+
π
3
)的图象按向量
a
平移后所得的图象关于点(-
π
12
，0)中心对称，则向量α的坐标可能为（　　）
A．(-
π
12
，0)		B．(-
π
6
，0)		C．(
π
12
，0)		D．(
π
6
，0)
设平移向量
a
=(m，0)，
则函数按向量平移后的表达式为y=sin[2(x-m)+
π
3
]=sin(2x+
π
3
-2m)，
因为图象关于点(-
π
12
，0)中心对称，
故x=-
π
12
，代入得：sin[2(-
π
12
)+
π
3
-2m]=0，
π
6
-2m=kπ（k∈Z），
k=0得：m=
π
12
，
故选C．
练习册系列答案
相关题目
给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②将函数y=sin(2图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
③在△ABC中，若AB=2，AC=3，∠ABC=60°，则△ABC必为锐角三角形；
④在同一坐标系中，函数y=sinx的图象和函数y=
x
2
的图象有三个公共点．
其中真命题是
 
．（填出所有正确命题的序号）
将函数y=sin(6x+
π
4
)的图象上各点的横坐标伸长到原来的3倍，再向右平移
π
8
个单位，得到的函数的一个对称中心（　　）
将函数y=sin(x+
π
3
)的图象向右平移
π
6
个单位，再向上平移2个单位所得图象对应的函数解析式是
y=sin(x+
π
6
)+2
y=sin(x+
π
6
)+2
．
将函数y=sin(
1
2
x+
π
3
)的图象作如下那种变换，才能得到函数y=sin(
1
2
x)的图象（　　）

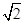要得到函数y=cos(2+)的图象, 只需要将函数y=sin(2+)图象上所有的点(     )

A．向左平移个单位，纵坐标不变；

B．向右平移个单位，纵坐标不变；

C．向左平移个单位，纵坐标不变；

D．向右平移 个单位，纵坐标不变．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网