题目内容
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是 那么这条斜线与平面所成的角是
____________
那么这条斜线与平面所成的角是
____________
【答案】

【解析】
试题分析:根据题意可知,由于已知平面的一条斜线和它在这个平面上的射影的方向向量分别是 ,那么结合向量的数量积公式可知,
,那么结合向量的数量积公式可知, ,可知向量的夹角为
,可知向量的夹角为 ,即为这条斜线与平面所成的角是
,即为这条斜线与平面所成的角是 。故答案为
。故答案为 。
。
考点:本试题考查了线面角的求解。
点评:对于斜线与平面所成的角冠军艾女士对于平面的射影的确定,然后结合法向量与平面的斜向量坐标关系,结合数量积公式得到夹角。属于基础题。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=(0,2,1),
=(
,
,
),那么这条斜线与平面的夹角是( )
| a |
| b |
| 2 |
| 5 |
| 5 |
| A、90° | B、60° |
| C、45° | D、30° |
如果平面的一条斜线和它在这个平面上的射影的方向向量分别是
=(1,0,1),
=(0,1,1),那么这条斜线与平面所成的角是( )
| a |
| b |
| A、90° | B、60° |
| C、45° | D、30° |
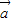 =(1,0,1),
=(1,0,1),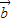 =(0,1,1),那么这条斜线与平面所成的角是( )
=(0,1,1),那么这条斜线与平面所成的角是( )