题目内容
设函数![]() (Ⅰ) 当
(Ⅰ) 当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性.(Ⅲ)若对任意
的单调性.(Ⅲ)若对任意![]() 及任意
及任意![]() ,恒有
,恒有
![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
(Ⅰ)函数的定义域为![]() . 当
. 当![]() 时,
时,![]()
![]() 2分
2分
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
![]() 无极大值.
无极大值. ![]() 4分
4分
(Ⅱ)![]()
![]()
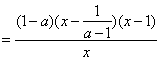
![]() 5分
5分
当![]() ,即
,即![]() 时,
时,![]()
![]() 在定义域上是减函数;
在定义域上是减函数;
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() 或
或![]()
令![]() 得
得![]() 当
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() 或
或![]()
令![]() 得
得![]() 综上,当
综上,当![]() 时,
时,![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 单调递减,在
单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 单调递减,在
单调递减,在![]() 上单调递增;
上单调递增;![]() 8分
8分


练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
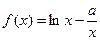 ,
,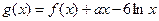 ,其中
,其中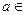 R
R 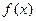 的单调性
的单调性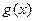 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数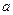 的取值范围
的取值范围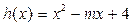 , 当
, 当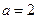 时,若
时,若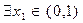 ,
,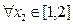 ,总有
,总有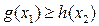 成立,求实数
成立,求实数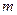 的取值范围
的取值范围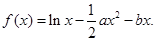
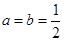 时,求函数
时,求函数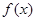 的最大值;
的最大值;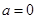 ,
,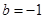 ,方程
,方程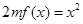 有唯一实数解,求正数
有唯一实数解,求正数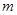 的值.
的值. ,
,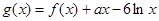 ,其中
,其中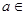 R.
R.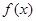 的单调性;
的单调性;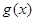 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数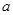 的取值范围;
的取值范围;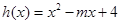 ,当
,当 时,若
时,若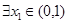 ,
,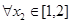 ,总有
,总有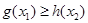 成立,求实数
成立,求实数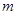 的取值范围.
的取值范围.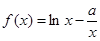 ,
,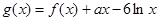 ,其中
,其中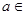 R.
R.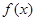 的单调性;
的单调性;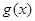 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数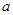 的取值范围;
的取值范围;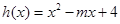 ,当
,当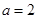 时,若
时,若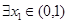 ,
,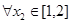 ,总有
,总有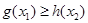 成立,求实数
成立,求实数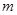 的取值范围.
的取值范围.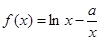 ,
,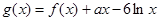 ,其中
,其中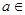 R.
R.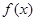 的单调性;
的单调性;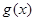 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数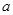 的取值范围;
的取值范围;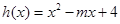 ,当
,当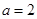 时,若
时,若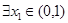 ,
,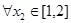 ,总有
,总有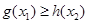 成立,求实数
成立,求实数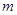 的取值范围.
的取值范围.