题目内容
已知向量 ,
, 满足|
满足| |=1,|
|=1,| |=2,
|=2, =-1,则
=-1,则 与
与 的夹角大小是
的夹角大小是
- A.60°
- B.90°
- C.120°
- D.150°
C
分析:设 与
与 的夹角为θ,根据两向量数量积的公式
的夹角为θ,根据两向量数量积的公式 =|
=| |•|
|•| |cosθ,变形得到cosθ=
|cosθ,变形得到cosθ= ,再将题中的数据代入,得cosθ=-
,再将题中的数据代入,得cosθ=- ,最后根据余弦函数在0°到180°的取值情况,可得θ=120°,即得向量
,最后根据余弦函数在0°到180°的取值情况,可得θ=120°,即得向量 与
与 的夹角大小.
的夹角大小.
解答:设 与
与 的夹角为θ,
的夹角为θ,
∵ =|
=| |•|
|•| |cosθ=-1
|cosθ=-1
∴cosθ= =
= =-
=-
∵0°≤θ≤180°
∴θ=120°
故选C
点评:本题以求两个特殊向量的夹角为载体,着重考查了平面向量的数量积的公式和两个向量夹角的求法,属于基础题.
分析:设
 与
与 的夹角为θ,根据两向量数量积的公式
的夹角为θ,根据两向量数量积的公式 =|
=| |•|
|•| |cosθ,变形得到cosθ=
|cosθ,变形得到cosθ= ,再将题中的数据代入,得cosθ=-
,再将题中的数据代入,得cosθ=- ,最后根据余弦函数在0°到180°的取值情况,可得θ=120°,即得向量
,最后根据余弦函数在0°到180°的取值情况,可得θ=120°,即得向量 与
与 的夹角大小.
的夹角大小.解答:设
 与
与 的夹角为θ,
的夹角为θ,∵
 =|
=| |•|
|•| |cosθ=-1
|cosθ=-1∴cosθ=
 =
= =-
=-
∵0°≤θ≤180°
∴θ=120°
故选C
点评:本题以求两个特殊向量的夹角为载体,着重考查了平面向量的数量积的公式和两个向量夹角的求法,属于基础题.

练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则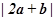 的值为_______.
的值为_______.