题目内容
三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3。

(1)求证:AB⊥BC ;
(2)如果AB=BC=2 ,求AC与侧面PAC所成角的大小。
,求AC与侧面PAC所成角的大小。
(2)如果AB=BC=2
 ,求AC与侧面PAC所成角的大小。
,求AC与侧面PAC所成角的大小。| 解:(1)取AC中点O,连结PO、BO ∵PA=PC ∴PO⊥AC 又∵侧面PAC⊥底面ABC ∴PO⊥底面ABC 又PA=PB=PC ∴AO=BO=CO ∴△ABC为直角三角形 ∴AB⊥BC。 (2)取BC的中点为M,连结OM,PM, 所以有OM=  AB= AB= ,AO= ,AO= ∴  由(1)有PO⊥平面ABC,OM⊥BC, 由三垂线定理得PM⊥BC ∴平面POM⊥平面PBC, 又∵PO=OM=  ∴△POM是等腰直角三角形,取PM的中点N,连结ON,NC 则ON⊥PM, 又∵平面POM⊥平面PBC,且交线是PM, ∴ON⊥平面PBC ∴∠ONC即为AC与平面PBC所成的角  ∴  ∴  故AC与平面PBC所成的角为  。 。 |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.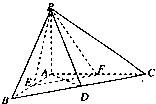 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,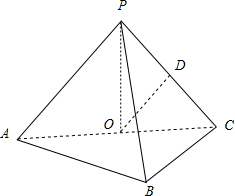 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.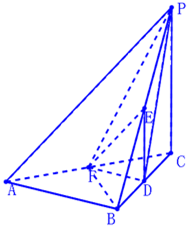 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.