题目内容
(本题满分12分)
已知各项均为正数的数列{an}满足2a2n+1+3an+1an-2a2n=0(n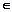
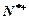 )且a3+
)且a3+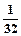 是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
(1)求数列{an}与{bn}的通项公式;
(2)若Tn=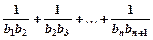 ,求证:Tn<
,求证:Tn<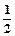
(3)若cn=-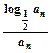 ,T/n=c1+c2+…+cn,求使T/n+n
,T/n=c1+c2+…+cn,求使T/n+n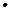 2n+1>125成立的正整数n的最小值
2n+1>125成立的正整数n的最小值
(1)∵2 a2n+1+3
a2n+1+3 ∴(an+1+2an)(2an+1-an)=0,∵{an}的各项均为正数,∴2an+1-an="0 " 即:an+1=
∴(an+1+2an)(2an+1-an)=0,∵{an}的各项均为正数,∴2an+1-an="0 " 即:an+1= ,∴{an}是以
,∴{an}是以 为公比的等比数列,由a2+a4=2a3+
为公比的等比数列,由a2+a4=2a3+ 得。
得。
a1=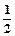 ∴an=(
∴an=( 又由Sn=n2得bn=2n-1
又由Sn=n2得bn=2n-1
(2)Tn= ∴Tn<
∴Tn<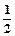
(3)由cn=-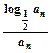 ,得cn=-n•2n≥
,得cn=-n•2n≥
得T/=(1-n)2n+1-2, 解答n≥6.
解析

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围