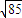题目内容
已知P是椭圆 上的点,若PF1⊥PF2,(其中F1、F2是椭圆的左、右焦点),则这样的点P有
上的点,若PF1⊥PF2,(其中F1、F2是椭圆的左、右焦点),则这样的点P有
- A.0个
- B.2个
- C.4个
- D.8个
B
分析:由题意可得:点P在以F1F2为直径的圆上.由椭圆的方程可得圆的直径为 ,并且椭圆的短半轴长也为
,并且椭圆的短半轴长也为 ,所以只有点P落在短轴顶点时满足题意.
,所以只有点P落在短轴顶点时满足题意.
解答:因为PF1⊥PF2,
所以点P在以F1F2为直径的圆上.
由椭圆的方程 可得圆的直径为2
可得圆的直径为2 ,
,
又因为椭圆的短半轴长也为 ,
,
所以只有点P落在短轴顶点时满足PF1⊥PF2,
所以这样的点P有2个.
故选B.
点评:本题主要考查椭圆的简单性质,以及圆的有关性质.
分析:由题意可得:点P在以F1F2为直径的圆上.由椭圆的方程可得圆的直径为
 ,并且椭圆的短半轴长也为
,并且椭圆的短半轴长也为 ,所以只有点P落在短轴顶点时满足题意.
,所以只有点P落在短轴顶点时满足题意.解答:因为PF1⊥PF2,
所以点P在以F1F2为直径的圆上.
由椭圆的方程
 可得圆的直径为2
可得圆的直径为2 ,
,又因为椭圆的短半轴长也为
 ,
,所以只有点P落在短轴顶点时满足PF1⊥PF2,
所以这样的点P有2个.
故选B.
点评:本题主要考查椭圆的简单性质,以及圆的有关性质.

练习册系列答案
相关题目
 上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若 ,则
,则 的面积为(
)
的面积为(
) B、2
B、2
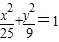 上的点,Q、R分别是圆
上的点,Q、R分别是圆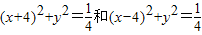 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )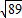
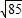
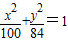 上的点,Q、R分别是圆(x+4)2+y2=1和圆(x-4)2+y2=1 上的点,则|PQ|+|PR|的最小值是( )
上的点,Q、R分别是圆(x+4)2+y2=1和圆(x-4)2+y2=1 上的点,则|PQ|+|PR|的最小值是( )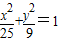 上的点,Q、R分别是圆
上的点,Q、R分别是圆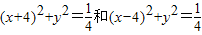 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )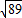
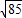
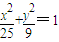 上的点,Q、R分别是圆
上的点,Q、R分别是圆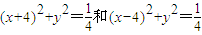 上的点,则|PQ|+|PR|的最小值是( )
上的点,则|PQ|+|PR|的最小值是( )