题目内容

如图所示的茎叶图记录了甲、乙两个小组（每小组4人）在期末考试中的数学成绩．乙组记录中有一个数据模糊，无法确认，在图中以a表示．已知甲、乙两个小组的数学成绩的平均分相同．
（1）求a的值；
（2）求乙组四名同学数学成绩的方差；
（3）分别从甲、乙两组同学中各随机选取一名同学，记这两名同学数学成绩之差的绝对值为X，求随机变量X的分布列和均值（数学期望）．

解：（1）依题意，∵甲、乙两个小组的数学成绩的平均分相同
∴ $\text{[math]}$ ，…（1分）
解得a=3．…（2分）
（2）根据已知条件，可以求得两组同学数学成绩的平均分都为 $\text{[math]}$ ．…（3分）
所以乙组四名同学数学成绩的方差为 $\text{[math]}$ ．
…（5分）
（3）分别从甲、乙两组同学中各随机选取一名同学，共有4×4=16种可能的结果．…（6分）
这两名同学成绩之差的绝对值X的所有情况如下表：

	87	89	96	96
87	0	2	9	9
93	6	4	3	3
93	6	4	3	3
95	8	6	1	1

所以X的所有可能取值为0，1，2，3，4，6，8，9．…（8分）
由表可得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
所以随机变量X的分布列为：

X	0	1	2	3	4	6	8	9
P	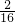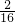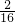$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

随机变量X的数学期望为 $\text{[math]}$ $\text{[math]}$ = $\text{[math]}$ ．…（12分）
分析：（1）根据甲、乙两个小组的数学成绩的平均分相同，建立方程，即可求得a的值；
（2）根据已知条件，可以求得两组同学数学成绩的平均分，进而可求乙组四名同学数学成绩的方差；
（3）分别从甲、乙两组同学中各随机选取一名同学，共有4×4=16种可能的结果，求出两名同学成绩之差的绝对值X的所有可能取值，求出相应的概率，从而可得随机变量X的分布列和均值
点评：本小题主要考查统计、方差、随机变量的分布列、均值（数学期望）等知识，考查或然与必然的数学思想方法，以及数据处理能力、运算求解能力和应用意识．