题目内容
(本小题满分14分)
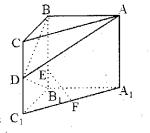
如图,在直三棱柱ABC—A1B1C1中,∠ ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
(1)求证:B1D⊥平面ABD;
(2)求异面直线BD与EF所成的角;
(3)求点F到平面ABD的距离。
如图,在直三棱柱ABC—A1B1C1中,∠
 ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。
ABC=90°,BC=2,AB=4,CC1=4,E在BB1上,且EB1=1,D、F分别为CC1、A1C1的中点。(1)求证:B1D⊥平面ABD;
(2)求异面直线BD与EF所成的角;
(3)求点F到平面ABD的距离。

(1)略
(2)BD与EF所成的角为
(3)
(2)BD与EF所成的角为

(3)

解:(1)由条件得
 ,
,
又 面BCC1B,
面BCC1B,
 面ABD…………3分
面ABD…………3分
(2)取B1C1的中点G,连接GE、GF,则EG//BD,
 或其补角为BD、EF所成角…………4分
或其补角为BD、EF所成角…………4分
 面BCC1B1,GF//A1B1
面BCC1B1,GF//A1B1
 面BCC1B1,
面BCC1B1,
在 中,
中,
 与EF所成角为
与EF所成角为 …………8
…………8 分
分
(3)设F到面ABD的距离为 ,作B作BH
,作B作BH AC于H,则BH
AC于H,则BH 面ACC1A1
面ACC1A1


 …………12分
…………12分

 ,
,又
 面BCC1B,
面BCC1B,
 面ABD…………3分
面ABD…………3分(2)取B1C1的中点G,连接GE、GF,则EG//BD,
 或其补角为BD、EF所成角…………4分
或其补角为BD、EF所成角…………4分 面BCC1B1,GF//A1B1
面BCC1B1,GF//A1B1 面BCC1B1,
面BCC1B1,
在
 中,
中,
 与EF所成角为
与EF所成角为 …………8
…………8 分
分(3)设F到面ABD的距离为
 ,作B作BH
,作B作BH AC于H,则BH
AC于H,则BH 面ACC1A1
面ACC1A1

 …………12分
…………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B
B

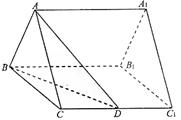
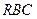 ,其中∠
,其中∠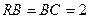 .点
.点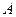 、
、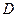 分别是
分别是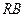 、
、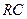 的中点,现将△
的中点,现将△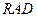 沿着边
沿着边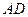 折起到△
折起到△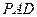 位置,使
位置,使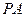 ⊥
⊥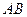 ,连结
,连结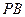 、
、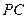 .
.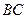 ⊥
⊥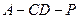 的余弦值.
的余弦值.
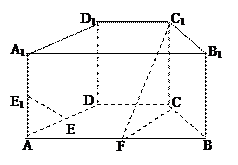
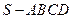 中,底面
中,底面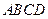 为正方形,侧棱
为正方形,侧棱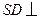 底面
底面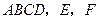 分别为
分别为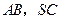 的中点.
的中点.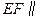 平面
平面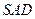 ;
;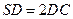 ,求二面角
,求二面角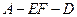 的大小.
的大小.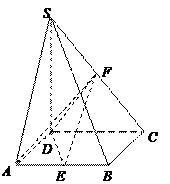
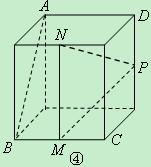
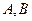 为正方形的两个顶点,
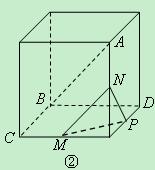
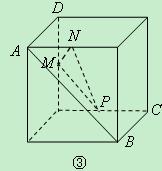
为正方形的两个顶点,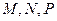 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出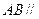 面
面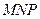 的图形的序号是 .(写出所有符合要求的图形序号)
的图形的序号是 .(写出所有符合要求的图形序号)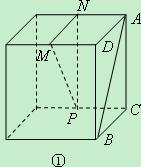
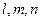 为不同的直线,
为不同的直线,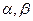 为不同的平面,有如下四个命题:
为不同的平面,有如下四个命题: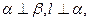 则
则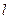 ∥
∥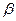 ②若
②若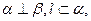 则
则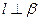
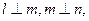 则
则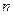 ④若
④若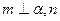 ∥
∥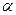 ∥
∥