题目内容
考察下列每组对象能否构成一个集合?(1)美丽的小鸟;
(2)不超过20的非负数;
(3)3、x、x2这三个实数.
解:(1)“美丽的小鸟”无明确标准,对于某个小鸟是否是“美丽的”无法给出明确的判断,即元素不具备确定性,因此(1)不能构成集合;
(2)任给一个实数x,可以明确地判断是不是“不超过20的非负数”,即“0≤x≤
(3)虽然三个实数已被指定,但这三个实数却不一定能构成集合,因为3、x、x2之间有可能相等,所以不一定满足元素的互异性.如果添加条件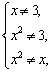 即x≠3且x≠±
即x≠3且x≠±![]() 且x≠0且x≠1,那么三个实数3、x、x2就可以构成一个集合.
且x≠0且x≠1,那么三个实数3、x、x2就可以构成一个集合.
点评:集合中的元素一定具有确定性、互异性、无序性;反过来,一组对象若不具备这三个特性,则这组对象也就不能构成集合.因此,在分析、处理集合问题的过程中,要时刻注意集合元素的三个特征对集合元素的限制.

练习册系列答案
相关题目