题目内容
【题目】已知数列![]() 的通项公式是
的通项公式是![]() .
.
(1)判断![]() 是否是数列
是否是数列![]() 中的项;
中的项;
(2)试判断数列![]() 中的各项是否都在区间
中的各项是否都在区间![]() 内;
内;
(3)试判断在区间![]() 内是否有无穷数列
内是否有无穷数列![]() 中的项?若有,是第几项?若没有,请说明理由.
中的项?若有,是第几项?若没有,请说明理由.
【答案】(1)![]() 不是数列
不是数列![]() 中的项;(2)
中的项;(2)![]() 中的各项都在区间
中的各项都在区间![]() 内;(3)区间
内;(3)区间![]() 内有数列
内有数列![]() 中的项,且只有一项,是第2项:
中的项,且只有一项,是第2项:![]() .
.
【思路分析】(1)解方程![]() ,求得
,求得![]() 的值,不为整数,所以
的值,不为整数,所以![]() 不是数列
不是数列![]() 中的项;(2)化简得
中的项;(2)化简得![]() ,再根据
,再根据![]() 可得
可得![]() ,即得数列
,即得数列![]() 中的项都在区间
中的项都在区间![]() 内;(3)解不等式
内;(3)解不等式![]() 可得
可得![]() .
.
【解析】(1)由题可得![]() ,
,
令![]() ,解得
,解得![]() .
.
因为![]() 不是正整数,所以
不是正整数,所以![]() 不是数列
不是数列![]() 中的项.(3分)
中的项.(3分)
(2)因为![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以数列![]() 中的各项都在区间
中的各项都在区间![]() )内.(6分)
)内.(6分)
(3)令![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() .
.
又![]() ,所以
,所以![]() .
.
故区间![]() 内有数列
内有数列![]() 中的项,且只有一项,是第2项:
中的项,且只有一项,是第2项:![]() .(10分)
.(10分)

【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 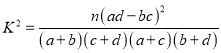 ,
,
【题目】“开门大吉”是某电视台推出的游戏节目,选手面对1![]() 号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段:
号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,在一次场外调查中,发现参赛选手多数分为两个年龄段: ![]() ;
; ![]() (单位:岁),其猜对歌曲名称与否的人数如图所示.
(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ)写出![]() 列联表;判断是否有
列联表;判断是否有![]() 的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
的把握认为猜对歌曲名称是否与年龄有关;说明你的理由;(如表的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(Ⅱ)现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手,并抽取3名幸运选手,求3名幸运选手中恰好有一人在![]() 岁之间的概率.
岁之间的概率.
(参考公式:  ,其中
,其中![]() )
)