题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
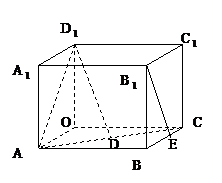
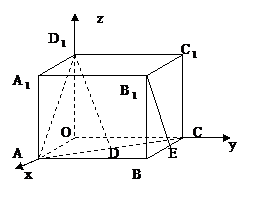
解(1)以O为坐标原点,建立如图所示空间直角坐标系.
∵|OA|=2,|AB|=3,|AA1|=2,E为BC的中点, ∴A(2,0,0),B(2,3,2),O1(0,0,2),E(1,3,0). 故 设< 则cos 故直线AO1与B1E所成角为arccos |
(2) |
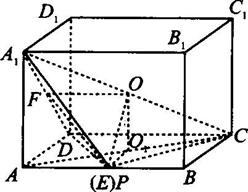
连结OD. ∵O1D⊥AC,∴OD⊥AC.设D(x,y,0), 由 得 解得: ∴点D的坐标为( 故O1D=| |

练习册系列答案
相关题目


 =
=

 或
或 =
=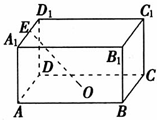 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于