题目内容
(本题满分16分)
已知数列 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为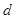 的等差数列;
的等差数列; 是公差为
是公差为 的等差数列(
的等差数列( ).
).
(Ⅰ)若 = 30,求
= 30,求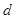 ;
;
(Ⅱ)试写出a30关于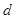 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得 是公差为
是公差为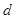 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出 关于
关于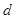 的关系式(
的关系式( N
N );
);
(Ⅳ)在(Ⅲ)条件下,且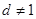 ,试用
,试用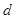 表示此数列的前100项和
表示此数列的前100项和
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
(Ⅲ)
(Ⅳ)
 。
。
解析试题分析:(Ⅰ)

于是,
(Ⅱ)


因此,
(Ⅲ)

(Ⅳ)



 +
+

考点:本题主要考查等差数列的通项公式,等差数列、等比数列的求和。
点评:中档题,等比数列、等差数列相关内容,已是高考必考内容,其难度飘忽不定,有时突出考查求和问题,如“分组求和法”、“裂项相消法”、“错位相减法”等,有时则突出涉及数列的证明题。本题解法中,利用了“分组求和法”。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为等差数列,
为等差数列, 为数列
为数列 项和,已知
项和,已知 .
.  ,求数列
,求数列 的前
的前 .
. 满足
满足 ,
, ;数列
;数列 满足
满足 ,
,  .
. 和
和 的通项公式;
的通项公式; 、
、 的前
的前 项和
项和 ,
, .
. 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立. 的取值范围;
的取值范围; ,
, ,求证:对任意的
,求证:对任意的 .
. ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0. , a1=1,a2=
, a1=1,a2= ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+ } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项.  是一个等差数列,且
是一个等差数列,且 ,
, .
. ; (Ⅱ)求
; (Ⅱ)求
 的最小值.
的最小值. 的前
的前 项和为
项和为 ,前
,前 项和为
项和为 .
.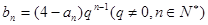 , 求数列
, 求数列 的前
的前 项和
项和 .
. bn=1.
bn=1. ;
;