题目内容
有限数列A={a1,a2,a3,…an},Sn是其前n项和,定义:
为A的“凯森和”,如有99项的数列A={a1,a2,a3,…a99}的“凯森和”为1000,则有100项的数列{1,a1,a2,a3,…a99}的“凯森和”为( )
| S1+S2+S3+…+Sn |
| n |
| A.1001 | B.991 | C.999 | D.990 |
设凯森和由Tn来表示,
由题意知A的T99=1000,
设新的凯森和为Tx,则100Tx=1×100+99×T99,解得Tx=991
故选B
由题意知A的T99=1000,
设新的凯森和为Tx,则100Tx=1×100+99×T99,解得Tx=991
故选B

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
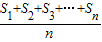 为A的“凯森和”,如有99项的数列A={a1,a2,a3,…a99}的“凯森和”为1000,则有100项的数列{1,a1,a2,a3,…a99}的“凯森和”为( )
为A的“凯森和”,如有99项的数列A={a1,a2,a3,…a99}的“凯森和”为1000,则有100项的数列{1,a1,a2,a3,…a99}的“凯森和”为( )