题目内容
已知F是抛物线y2=4x的焦点,P是圆x2+y2-8x-8y+31=0上的动点,则|FP|的最小值是( )
(A)3 (B)4 (C)5 (D)6
【答案】
B
【解析】圆x2+y2-8x-8y+31=0的圆心C坐标为(4,4),半径为1,
∵|PF|≥|CF|-1,
∴当P、C、F三点共线时,|PF|取到最小值,
由y2=4x知F(1,0),
∴|PF|min=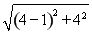
-1=4.
故选B.
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知F是抛物线y2=x的焦点，A，B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到y轴的距离为（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
（2010•重庆一模）已知F是抛物线y2=4x的焦点，Q是抛物线的准线与x轴的交点，直线l经过点Q．