题目内容
我国1990&2000年的国内生产总值如下表所示:年份x | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
产值y/亿元 | 18 598.4 | 21 662.5 | 26 651.9 | 34 560.5 | 46 670.0 | 57 494.9 | 6 6850.5 | 73 142.7 | 76 967.1 | 80 422.8 | 89 404.0 |
(1)描点画出1990&2000年国内生产总值的图像;
(2)建立一个能基本反映这一时期国内生产总值发展变化的函数模型,并根据这个模型,预测2020年的国内生产总值.
解析:画出散点图,观察函数类型.
解:(1)作散点图(略).
(2)由散点图,可知函数为y=a+bx,
![]() =1xi=21 945,
=1xi=21 945,![]() =592 425.3,
=592 425.3,![]() =43 780 385,
=43 780 385,
![]() =1 182 725 833,
=1 182 725 833,![]() =1 995,
=1 995,![]() =53 856.845,
=53 856.845,
b=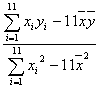 =
=![]() =7 612.359 1,
=7 612.359 1,
a=![]() -b
-b![]() =53 856.845-7 612.359 1×1 995=-15 132 799.56,
=53 856.845-7 612.359 1×1 995=-15 132 799.56,
∴y=-15 132 799.56+7 612.359 1x.当x=2 020时,y=244 165.822亿元,
即预测2020年国民生产总值约为244 165.822亿元.

 阅读快车系列答案
阅读快车系列答案年份 | 1990 | 1991 | 1992 | 1993 |
产值/亿元 | 18 598.4 | 21 662.5 | 26 651.9 | 34 560.5 |
年份 | 1994 | 1995 | 1996 | 1997 |
产值/亿元 | 46 670.0 | 57 494.9 | 66 850.5 | 73 142.7 |
年份 | 1998 | 1999 | 2000 |
|
产值/亿元 | 76 967.1 | 80 422.8 | 89 404.0 |
|
(1)描点画出1990—2000年国内生产总值的图象;
(2)建立一个能基本反映这一时期国内生产总值发展变化的函数模型,并画出其图象;
(3)根据所建立的函数模型,预测2004年的国内生产总值.
年份 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
产值/亿元 | 18 598.4 | 21 662.5 | 26 651.9 | 34 560.5 | 46 670.0 | 57 494.9 | 66 850.5 | 73 142.7 | 76 967.1 | 80 422.8 | 89 404.0 |
则反映这一时期国内生产总值发展变化的函数模型可能为( )
A.y=aekx B.y=a+bx C.y=axb D.y=![]()
年份 | 1990 | 1991 | 1992 | 1993 |
产值/亿元 | 18 598.4 | 21 662.5 | 26651.9 | 34 560.5 |
年份 | 1994 | 1995 | 1996 | 1997 |
产值/亿元 | 46 670.0 | 57 494.9 | 66 850.5 | 73 142.7 |
年份 | 1998 | 1999 | 2000 |
|
产值/亿元 | 76 967.1 | 80 422.8 | 89 404.0 |
|
则反映这一时期国内生产总值发展变化的函数模型可能为( )
A.y=aekx B.y=a+bx
C.y=axb D.y=ae![]()
 ; 县镇:
; 县镇: ;农村:
;农村: .
.