题目内容
(Ⅰ)已知函数f(x)=-3x2+6x-2.Sn是数列{an}的前n项和,点(n,Sn)(n∈N*)在曲线y=f(x)+2上,求an;(Ⅱ)在(Ⅰ)的条件下,若bn=(![]() )n-1,cn=
)n-1,cn=![]() ,且Tn是数列{cn}的前n项和.试问Tn是否存在最大值?若存在,请求出Tn的最大值,若不存在,请说明理由.
,且Tn是数列{cn}的前n项和.试问Tn是否存在最大值?若存在,请求出Tn的最大值,若不存在,请说明理由.
(Ⅰ)点(n,Sn)在曲线y=f(x)+2上,所以Sn=-3n2+6n.
当n=1时,a1=S1=3,当n≥2时,an=Sn-Sn-1=9-6n,
∴an=9-6n.
(Ⅱ)∵bn=(![]() )n-1,
)n-1,
cn=![]() anbn=
anbn=![]() (
(![]() )n-1=(3-2n)(
)n-1=(3-2n)(![]() )n,
)n,
∴Tn=c1+c2+…+cn
=![]() -(
-(![]() )2+…+(3-2n)(
)2+…+(3-2n)(![]() )n.
)n.
利用错位相减法,∴Tn=(2n+1)(![]() )n-1.
)n-1.
∵Tn+1=(2n+1)(![]() )n>0,Tn+1+1
)n>0,Tn+1+1
=(2n+3)(![]() )n+1>0,
)n+1>0,
∵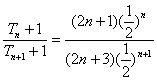 >1,
>1,
∴Tn+1+1<Tn+1,
∴Tn+1<Tn<…<T1=![]() .
.
存在最大值T1=![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|