题目内容
是否存在实数p,使4x+P<0是x2-x-2>0的充分条件?如果存在,求出P的取值范围;否则,说明理由.
【答案】分析:解不等式x2-x-2>0,将其解集表示为A,解不等式4x+P<0,将其解集表示为B,若存在满足条件的P,则B⊆A,根据集合间包含关系的运算,我们易得到一个关于P的不等式,解不等式即可求出P的取值范围.
解答:解:由x2-x-2>0,解得x>2或x<-1,
令A={x|x>2或x<-1},(3分)
由4x+p<0,得B= ,(6分)
,(6分)
当B⊆A时,即 ,即p≥4,(10分)
,即p≥4,(10分)
此时 ,(12分)
,(12分)
∴当p≥4时,4x+p<0是x2-x-2>0的充分条件.(14分)
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,根据充要条件的定义,将问题转化为一个集合之间包含关系是判断是解答本题的关键.
解答:解:由x2-x-2>0,解得x>2或x<-1,
令A={x|x>2或x<-1},(3分)
由4x+p<0,得B=
 ,(6分)
,(6分)当B⊆A时,即
 ,即p≥4,(10分)
,即p≥4,(10分)此时
 ,(12分)
,(12分)∴当p≥4时,4x+p<0是x2-x-2>0的充分条件.(14分)
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,根据充要条件的定义,将问题转化为一个集合之间包含关系是判断是解答本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 为该平面上一动点,作
为该平面上一动点,作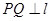 ,垂足为Q,且(
,垂足为Q,且(
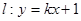 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由 .
.