Question

已知关于t的一元二次方程t²+(2+i)t+2xy+(x-y)i=0(x、y∈R).?

       (1)当方程有实数根时,求点(x,y)的轨迹方程.?

       (2)求方程实根的取值范围.?

      

Answer 1

思路分析:方程有实根,即说明t、x、y∈R,利用复数相等可解出t、x、y之间的关系,再消去t得x、y的等量关系,即为轨迹方程.

       解:(1)设实根t,则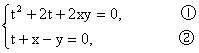

       由②得t=y-x,代入①得(y-x)²+2(y-x)+2xy=0,?

       即(x-1)²+(y+1)²=2.③?

       ∴所求点的轨迹方程为(x-1)²+(y+1)²=2,轨迹是以(1,-1)为圆心,2为半径的圆.?

       (2)由③得圆心为(1,-1),半径r=.?

       直线t=y-x与圆有公共点,有,?

       即|t+2|≤2,∴-4≤t≤0.?

       故方程的实根的取值范围是［-4,0］.