题目内容
 过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点,设切线AP、AQ的斜率分别为k1和k2.
过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点,设切线AP、AQ的斜率分别为k1和k2.(Ⅰ)求证:k1k2=-4;
(Ⅱ)求证:直线PQ恒过定点,并求出此定点坐标.
分析:(Ⅰ)设出切线的方程代入抛物线,消去y可得x2-kx+(ka+1)=0,利用判别式等于0,即可证得结论;
(Ⅱ)确定切线AP、AQ的方程,从而可得直线PQ的方程,即可得到直线PQ过定点.
(Ⅱ)确定切线AP、AQ的方程,从而可得直线PQ的方程,即可得到直线PQ过定点.
解答:证明:(Ⅰ)设过A(a,0)与抛物线y=x2+1的相切的直线的斜率是k,
则该切线的方程为:y=k(x-a),代入抛物线,消去y可得x2-kx+(ka+1)=0
∴△=k2-4(ka+1)=k2-4ak-4=0
∴k1,k2都是方程k2-4ak-4=0的解,∴k1k2=-4
(Ⅱ)设P(x1,y1),Q(x2,y2)
由于y'=2x,故切线AP的方程是:y-y1=2x1(x-x1)
则-y1=2x1(a-x1)=2x1a-2x12=2x1a-2(y1-1),∴y1=2x1a+2,
同理y2=2x2a+2
∴直线PQ的方程是y=2ax+2,
∴直线PQ过定点(0,2).
则该切线的方程为:y=k(x-a),代入抛物线,消去y可得x2-kx+(ka+1)=0
∴△=k2-4(ka+1)=k2-4ak-4=0
∴k1,k2都是方程k2-4ak-4=0的解,∴k1k2=-4
(Ⅱ)设P(x1,y1),Q(x2,y2)
由于y'=2x,故切线AP的方程是:y-y1=2x1(x-x1)
则-y1=2x1(a-x1)=2x1a-2x12=2x1a-2(y1-1),∴y1=2x1a+2,
同理y2=2x2a+2
∴直线PQ的方程是y=2ax+2,
∴直线PQ过定点(0,2).
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.注意设而不求方法的运用.

练习册系列答案
相关题目
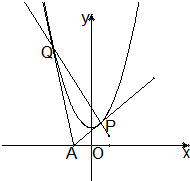 过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点,设切线AP,AQ的斜率分别为k1和k2.
过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点,设切线AP,AQ的斜率分别为k1和k2.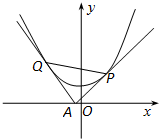 过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点.
过x轴上动点A(a,0)引抛物线y=x2+1的两条切线AP、AQ,P、Q为切点.