题目内容
(本小题满分12分)已知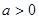 ,函数
,函数
(1)当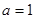 时,求函数
时,求函数 在点(1,
在点(1,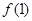 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使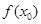 >g(xo)成立,求正实数
>g(xo)成立,求正实数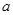 的取值范围。
的取值范围。
【答案】
(Ⅰ)
函数 在点(1,
在点(1,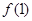 )的切线方程为
)的切线方程为 ;
;
(Ⅱ)当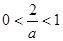 即
即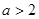 时,
时, 的极大值是
的极大值是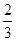 ,极小值是
,极小值是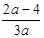
①
当 即
即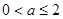 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为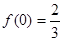 ,无极小值。
,无极小值。
综上所述 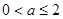 时,极大值为
时,极大值为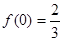 ,无极小值
,无极小值
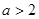 时 极大值是
时 极大值是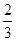 ,极小值是
,极小值是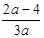
(Ⅲ)(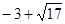
 ,
,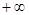 ) .
) .
【解析】本试题主要考查了导数在研究函数中的运用。 利用导数的几何意义求解切线方程,并结合导数的符号与单调性的关系,求解函数的极值,并分析方程根的问题的综合运用。
(1)先求解函数定义域和导数,然后得到切点处的导数值即为切线的斜率,利用点斜式得到方程。
(2)因为 是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。
是关于含有参数的二次函数形式,那么对于参数a分情况讨论得到单调性和极值问题。
(3)构造新的函数设 ,
, ,利用导数的思想求解其最大值即可。便可以得到a的范围。
,利用导数的思想求解其最大值即可。便可以得到a的范围。
解:(Ⅰ)∵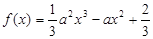 ∴
∴ 
∴ 当 时,
时,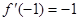 又
又 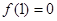
∴ 函数 在点(1,
在点(1,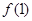 )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令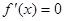 有
有 
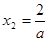
②
当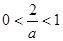 即
即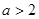 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是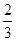 ,极小值是
,极小值是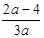
③
当 即
即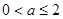 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为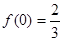 ,无极小值。
,无极小值。
综上所述 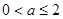 时,极大值为
时,极大值为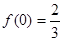 ,无极小值
,无极小值
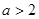 时 极大值是
时 极大值是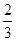 ,极小值是
,极小值是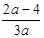 ----------8分
----------8分
(Ⅲ)设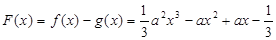 ,
,
对 求导,得
求导,得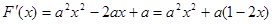
∵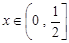 ,
,
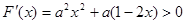
∴  在区间
在区间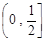 上为增函数,则
上为增函数,则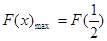
依题意,只需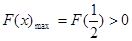 ,即
,即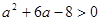
解得 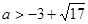 或
或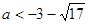 (舍去)
(舍去)
则正实数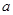 的取值范围是(
的取值范围是(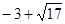
 ,
,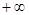 ) ----------12分
) ----------12分

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
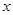
 )
)


