题目内容
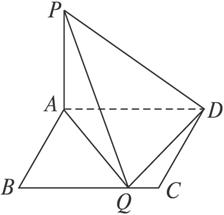
如图2-3-34,矩形纸片AA′A1′A1,B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成正三棱柱,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
图2-3-34
思路分析:补形法,恢复成一个直四棱柱.
证明:作AD∥BC,BD∥AC交于D,作A1D1∥B1C1,B1D1∥A1C1交于D1,连结BD1、DD1.
∵A1D1B1C1为菱形,∴A1B1⊥D1C1.
又AA1⊥平面A1D1B1C1,
∴AA1⊥D1C1,从而D1C1⊥平面ABB1A1,
∴D1C1⊥AB1.又AB1⊥BC1,∴AB1⊥平面BC1D1,
∴AB1⊥BD1.∵BD1∥CA1,∴AB1⊥A1C.
练习册系列答案
孟建平名校考卷系列答案
相关题目
=5e1,
=3e2,则
等于（ ）
（5e1+3e2） B.
（5e1-3e2） C.
（3e2-5e1） D.
（5e2-3e1）
=a，
=b，用a、b表示
=_____________.
=e1,
=e2,以e1、e2为基底，表示向量
、
、
及
.
