题目内容
如图，正四面体ABCD中，E在棱AB上，F在棱CD上，使得
=
=λ （0＜λ＜+∞），记f（λ）=αλ+βλ其中αλ表示EF与AC所成的角，βλ表示EF与BD所成的角，则（ ）
| AE |
| EB |
| CF |
| FD |
| A．f（λ）在（0，+∞）单调增加 |
| B．f（λ）在（0，+∞）单调减少 |
| C．f（λ） 在（0，1）单调增加，而在（1，+∞单调减少 |
| D．f（λ）在（0，+∞）为常数 |
作EG∥AC交BC于G，连GF，
则
=
=
，故GF∥BD
∴∠GEF=αλ，∠GFE=βλ，
取BD的中点M，连接AM，CM，∵ABCD是正四面体，∴BD⊥AM，BD⊥CM，
∵AM∩CM=M，∴BD⊥平面ACM
∵AC?平面ACM
∴AC⊥BD，∴∠EGF=90°
故f（λ）=）=αλ+βλ=∠GEF+∠GFE=90°，即为常数．
故选D．
则
| AE |
| EB |
| CG |
| GB |
| CF |
| FD |
∴∠GEF=αλ，∠GFE=βλ，
取BD的中点M，连接AM，CM，∵ABCD是正四面体，∴BD⊥AM，BD⊥CM，
∵AM∩CM=M，∴BD⊥平面ACM
∵AC?平面ACM
∴AC⊥BD，∴∠EGF=90°
故f（λ）=）=αλ+βλ=∠GEF+∠GFE=90°，即为常数．
故选D．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
9、如图，正四面体ABCD的顶点A，B，C分别在两两垂直的三条射线Ox，Oy，Oz上，则在下列命题中，错误的为（ ）
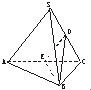如图，正四面体S-ABC中，D为SC的中点，则BD与SA所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
14、如图，正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上，给出下列四个命题：
如图：正四面体S-ABC中，如果E，F分别是SC，AB的中点，那么异面直线EF与SA所成的角等于（ ）
如图，正四面体S-ABC的边长为a，D是SA的中点，E是BC的中点，则SDE绕SE旋转一周所得旋转体的体积为