Question

设x，y满足约束条件

x≥2 2x-y≥1 y≥x

，若目标函数z=ax+by（a＞0，b＞0）的最小值为2，则ab的最大值为（　　）

• A、1
• B、

  1

  2

• C、

  1

  4

• D、

  1

  6

Answer 1

分析：画出满足约束条件

x≥2 2x-y≥1 y≥x

的可行域，结合目标函数z=ax+by（a＞0，b＞0）的最小值为2，进而由基本不等式可得答案．

解答：解：满足约束条件

x≥2 2x-y≥1 y≥x

的可行域如下图所示：

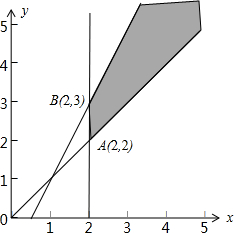
∵目标函数z=ax+by（a＞0，b＞0）
故z_A=2a+2b，z_B=2a+3b，
由目标函数z=ax+by（a＞0，b＞0）的最小值为2，
则2a+2b=2，即a+b=1
则ab≤(

a+b

2

)2=

1

4

故ab的最大值为

1

4

故选C

点评：本题考查的知识点是简单线性规划，基本不等式，是不等式的综合应用，难度中档．