Question

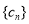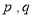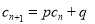对于给定数列，如果存在实常数使得对于任意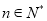都成立，我们称数列是 “线性数列”．

（1）若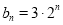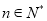，，，数列、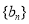是否为“线性数列”？若是，指出它对应的实常数，若不是，请说明理由；

（2）证明：若数列是“线性数列”，则数列也是“线性数列”；

（3）若数列满足，，为常数．求数列前项的和．

Answer 1

（1）见解析；（2）见解析；（3）.

【解析】

试题分析：（1）由 ，可得 ，可得数列{an}是“线性数列”，对应的实常数分别为1，2．同理数列 是“线性数列”．（2）利用“线性数列”的定义即可证明；（3）对n分奇数与偶数讨论，利用等比数列的前n项和公式即可得出．

试题解析：（1）【解析】
，∴数列 是“线性数列”，对应的实常数分别为1，2．∵ ， ，∴数列 是“线性数列”，对应的实常数分别为2，0．

（2）证明：若数列{an}是“线性数列”，则存在实常数p，q，使得 对于任意 都成立，

且有 对于任意 都成立，因此 对于任意 都成立，故数列 也是“线性数列”．对应的实常数分别为p，2q．

（3）【解析】
，

当n为偶数时，

，

当n为奇数时，

故数列 前n项的和 .

考点：数列的求和；数列递推式．