题目内容
由直线y=x+1上的一点向圆(x－3)2+y2=1引切线，则切线长的最小值为（ ）
| A．1 | B． | C．2 | D．3 |
B
解析试题分析： 根据题意可知切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得，圆心（3，0）到直线的距离为d=
，圆的半径为1，故切线长的最小值为
，故选B.
考点：本题主要考查了圆的切线方程，点到直线的距离，是基础题
点评：解决该试题的关键是先求圆心到直线的距离，此时切线长最小，由勾股定理不难求解切线长的最小值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若圆
上有且只有两个点到直线
的距离等于
，则半径
的取值范围是（ ）
A． | B． | C． | D． |
（ ）圆
关于直线
对称的圆的方程是
A． | B． |
C． | D． |
圆
和圆
的位置关系是( )
| A．外切 | B．内切 | C．外离 | D．内含 |
将圆
平分的直线是( )
A． | B． | C． | D． |
所表示的曲线的图形是（ ）
自点A（3，5）作圆C：
的切线，求切线的方程（ ）
A． | B． |
| C．或 | D．以上都不对 |
从点
向圆C:
引切线,则切线长的最小值为( )
A． | B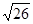． | C． | D．5 |
能够使得圆 
上恰有两个点到直线 
的距离等于1的 
的一个可能值为( )
| A．2 | B． | C．3 | D． |