题目内容
函数y=log
|x-3|的单调递减区间是 ．
【答案】分析：将原函数分解成两个简单函数，即y=
、u=|x-3|，根据复合函数单调性判断--同增异减得到答案．
解答：解：令u=|x-3|，则在（-∞，3）上u为x的减函数，在（3，+∞）上u为x的增函数．
又∵0＜
＜1，y=
是减函数
∴在区间（3，+∞）上，y为x的减函数．
故答案为：（3，+∞）
点评：本题主要考查复合函数的单调性，即同增异减性．这种是高考中经常考的题型，应给予重视．
、u=|x-3|，根据复合函数单调性判断--同增异减得到答案．解答：解：令u=|x-3|，则在（-∞，3）上u为x的减函数，在（3，+∞）上u为x的增函数．
又∵0＜
＜1，y=是减函数∴在区间（3，+∞）上，y为x的减函数．
故答案为：（3，+∞）
点评：本题主要考查复合函数的单调性，即同增异减性．这种是高考中经常考的题型，应给予重视．
练习册系列答案
名校课堂系列答案
相关题目
(x+
+1)(x＞1)的最大值为_____________.
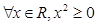”的否定是“
”；
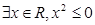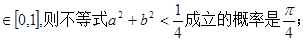
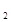(x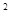
-ax+2)在
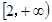上恒为正，则实数a的取值范围是