题目内容
已知函数f(x)=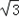 sin2x﹣2sin2x.
sin2x﹣2sin2x.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)求函数f(x)的零点的集合.
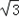 sin2x﹣2sin2x.
sin2x﹣2sin2x.(Ⅰ)求函数f(x)的最大值;
(Ⅱ)求函数f(x)的零点的集合.
解:(Ⅰ)∵f(x)=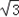 sin2x﹣2sin2x=
sin2x﹣2sin2x=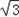 sin2x+cos2x﹣1=2sin(2x+
sin2x+cos2x﹣1=2sin(2x+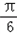 )﹣1
)﹣1
故函数f(x)的最大值等于2﹣1=1
(Ⅱ)由f(x)=0得2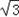 sin xcos x=2sin2x,
sin xcos x=2sin2x,
于是sin x=0,或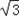 cos x=sin x
cos x=sin x
即tan x=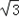
由sin x=0可知x=kπ;
由tan x=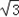 可知x=kπ+
可知x=kπ+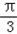 .
.
f(x)的零点的集合为{x|x=kπ或x=k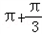 ,k∈Z}
,k∈Z}

练习册系列答案
相关题目
