题目内容
若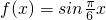
，则f（1）+f（3）+f（5）+…+f（2009）=________．
2
分析：由函数的解析式可以得出，函数值呈周期性变化，故先研究一个周期上的函数值的和，再依据其规律求和．
解答：∵f（1）+f（3）+f（5）+f（7）+f（9）+f（11）=0，
∴f（x）中每连续六项的和等于0，f（x）中共有1005项，
∵1005÷6=167…3，
∴
故答案为2
点评：本题考查三角函数的化简求值，解题的关键是研究出函数值周期性变化的规律，以此规律转化求值．
分析：由函数的解析式可以得出，函数值呈周期性变化，故先研究一个周期上的函数值的和，再依据其规律求和．
解答：∵f（1）+f（3）+f（5）+f（7）+f（9）+f（11）=0，
∴f（x）中每连续六项的和等于0，f（x）中共有1005项，
∵1005÷6=167…3，
∴
故答案为2
点评：本题考查三角函数的化简求值，解题的关键是研究出函数值周期性变化的规律，以此规律转化求值．
练习册系列答案
相关题目
，则f（1）+f（3）+f（5）+…+f（2011）= ．