题目内容
如图，在棱锥P－ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC＝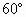
，M为PB的中点．
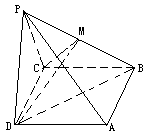
(Ⅰ)求证：PA⊥CD；
(Ⅱ)求二面角P－AB－D的度数；
(Ⅲ)求证：平面CDM⊥平面PAB；
(Ⅳ)求三棱锥B—CDM的体积．
答案：
解析：
解析：
|
(Ⅰ)证明：依条件得 ∴△ADC为等边三角形，又△PDC也为等边三角形．
设CD中点为H，连PH，AH， ∵PH⊥CD，AH⊥CD， ∴CD⊥面PHA，又 (Ⅱ)解：∵AB∥CD，由(Ⅰ)可知PA⊥AB，AH⊥AB， ∴∠PAH是二面角P－AB－D的平面角， ∵∠PHA＝ 即二面角P－AB－D的度数为 (Ⅲ)证明：设平面CDM与PA交于点N，连MN，HN， ∵AB∥CD，∴AB∥面CDNM，∴AB∥NM， ∵AB⊥PA∴MN⊥PA，① 又∵M是PB的中点，∴N是PA的中点， 又在△PHA中，∠PHA＝ 由①，②得：PA⊥面CDM，又 ∴面CDM⊥面PAB， (Ⅳ)解：(文科)∵ 又点M到面BCD的距离等于 ∴ (理科)∵ M为PB的中点，∴ ∴ ∵ |
面PHA，∴PA⊥CD，
，PH＝AH，∴∠PAH＝
，
面PAB，
，
PH，
，
，
练习册系列答案
相关题目
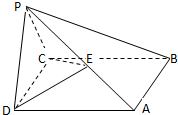如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，底面ABCD是菱形，且∠ADC=60°，E为PA的中点，二面角P-CD-A为120°．
如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点，
如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点，
