题目内容
如果30<x<42,16<y<24,则x-2y的取值范围是 ;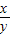 的取值范围是 .
的取值范围是 .
【答案】分析:先作出不等式组表示的平面区域,设z=x-2y可得,y= x-
x- z,则-
z,则- z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围;欲求
z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围;欲求 的取值范围,可先求
的取值范围,可先求 的取值范围,而
的取值范围,而 的几何意义表示点(x,y)与原点连线的斜率,利用直线的斜率求其取值范围.
的几何意义表示点(x,y)与原点连线的斜率,利用直线的斜率求其取值范围.
解答: 解:作出不等式组表示的平面区域
解:作出不等式组表示的平面区域
由z=x-2y可得,y= x-
x- z,则-
z,则- z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小
z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小
结合函数的图形可知,
当直线x-2y-z=0平移到A(30,24)时,截距最大,z最小Zmin=30-2×24=-18;
当直线x-2y-z=0平移到B(42,16)时,截距最小,z最大Zmax=42-2×16=10,
则z=x-2y∈(-18,10);
 的几何意义表示点(x,y)与原点连线的斜率,
的几何意义表示点(x,y)与原点连线的斜率,
利用直线的斜率求得其最大值kOA= ,最小值为kOB=
,最小值为kOB= ,
,
其取值范围( ,
, )
)
∴ 的取值范围是 (
的取值范围是 ( )
)
故答案为:(-18,10);( ).
).
点评:平面区域的范围问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.
 x-
x- z,则-
z,则- z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围;欲求
z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小,结合函数的图形可求z的最大与最小值,从而可求z的范围;欲求 的取值范围,可先求
的取值范围,可先求 的取值范围,而
的取值范围,而 的几何意义表示点(x,y)与原点连线的斜率,利用直线的斜率求其取值范围.
的几何意义表示点(x,y)与原点连线的斜率,利用直线的斜率求其取值范围.解答:
 解:作出不等式组表示的平面区域
解:作出不等式组表示的平面区域由z=x-2y可得,y=
 x-
x- z,则-
z,则- z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小
z表示直线x-2y-z=0在y轴上的截距,截距越大,z越小结合函数的图形可知,
当直线x-2y-z=0平移到A(30,24)时,截距最大,z最小Zmin=30-2×24=-18;
当直线x-2y-z=0平移到B(42,16)时,截距最小,z最大Zmax=42-2×16=10,
则z=x-2y∈(-18,10);
 的几何意义表示点(x,y)与原点连线的斜率,
的几何意义表示点(x,y)与原点连线的斜率,利用直线的斜率求得其最大值kOA=
 ,最小值为kOB=
,最小值为kOB= ,
,其取值范围(
 ,
, )
)∴
 的取值范围是 (
的取值范围是 ( )
)故答案为:(-18,10);(
 ).
).点评:平面区域的范围问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
相关题目