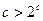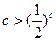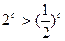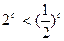题目内容
设a>0,a≠1,解关于x的不等式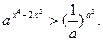
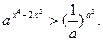
当0<a<1时,原不等式的解集为
{x|- <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};
当a>1时,原不等式的解集为 {x|-∞<x<+∞}..
{x|-
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};当a>1时,原不等式的解集为 {x|-∞<x<+∞}..
本小题考查指数函数性质、解不等式及综合分析能力.满分12分.
解法一 原不等式可写成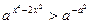 . ① ——1分
. ① ——1分
根据指数函数性质,分为两种情形讨论:
(Ⅰ)当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
由于0<a<1时,判别式
△=4-4a2>0,
所以②式等价于
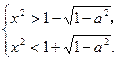 ——5分解③式得x<-
——5分解③式得x<- 或x>
或x> ,
,
解④式得- <x<
<x< . ——7分
. ——7分
所以,0<a<1时,原不等式的解集为
{x|- <x<-
<x<- }∪{x|
}∪{x| <x<
<x< }.
}.
——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑤ ——9分
由于a>1,判别式△<0,故⑤式对任意实数x成立,即得原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|- <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};
当a>1时,原不等式的解集为
{x|-∞<x<+∞}.
解法二 原不等式可写成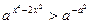 . ① ——1分
. ① ——1分
(Ⅰ) 当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
分解因式得 (x2-1+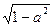 )(x2-1-
)(x2-1-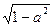 )<0. ③
)<0. ③
即 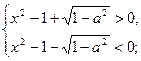
或 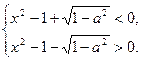 ——5分解由④、⑤组成的不等式组得
——5分解由④、⑤组成的不等式组得
- <x<-
<x<- .
.
或 <x<
<x< . ——7分
. ——7分
由⑥、⑦组成的不等式组解集为空集;所以,0<a<1时,原不等式的解集为
{x|- <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};
——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑧ ——9分
配方得 (x2-1)2+a2-1>0, ⑨
对任意实数x,不等式⑨都成立,即a>1时,原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|- <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};
当a>1时,原不等式的解集为 {x|-∞<x<+∞}.
解法一 原不等式可写成
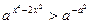 . ① ——1分
. ① ——1分根据指数函数性质,分为两种情形讨论:
(Ⅰ)当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
由于0<a<1时,判别式
△=4-4a2>0,
所以②式等价于
|
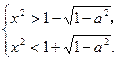 ——5分解③式得x<-
——5分解③式得x<- 或x>
或x> ,
,解④式得-
 <x<
<x< . ——7分
. ——7分所以,0<a<1时,原不等式的解集为
{x|-
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< }.
}.——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑤ ——9分
由于a>1,判别式△<0,故⑤式对任意实数x成立,即得原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|-
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};当a>1时,原不等式的解集为
{x|-∞<x<+∞}.
解法二 原不等式可写成
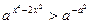 . ① ——1分
. ① ——1分(Ⅰ) 当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
分解因式得 (x2-1+
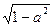 )(x2-1-
)(x2-1-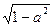 )<0. ③
)<0. ③
|
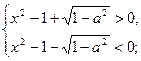
|
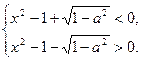 ——5分解由④、⑤组成的不等式组得
——5分解由④、⑤组成的不等式组得-
 <x<-
<x<- .
.或
 <x<
<x< . ——7分
. ——7分由⑥、⑦组成的不等式组解集为空集;所以,0<a<1时,原不等式的解集为
{x|-
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑧ ——9分
配方得 (x2-1)2+a2-1>0, ⑨
对任意实数x,不等式⑨都成立,即a>1时,原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|-
 <x<-
<x<- }∪{x|
}∪{x| <x<
<x< };
};当a>1时,原不等式的解集为 {x|-∞<x<+∞}.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
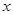 小时的收费为
小时的收费为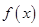 元
元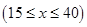 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动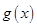 元
元 且
且 的图象恒过定点
的图象恒过定点 ,则
,则
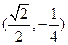 ,则a=
,则a=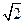
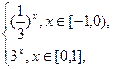 则f(log3
则f(log3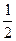 )=__________.
)=__________. 的解是
的解是
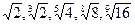 从小到大的排列顺序是 .
从小到大的排列顺序是 .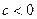 ,则下列不等式中成立的一个是 ()
,则下列不等式中成立的一个是 ()