题目内容
(本小题满12分) 已知函数![]()
(Ⅰ)将函数![]() 化简成
化简成![]() 的形式,并指出
的形式,并指出![]() 的周期;(Ⅱ)求函数
的周期;(Ⅱ)求函数![]() 上的最大值和最小值
上的最大值和最小值
(Ⅰ)同解析;(2)x=![]() 时,f(x)有最小值-
时,f(x)有最小值-![]() ;当x=π时,f(x)有最大值-2.
;当x=π时,f(x)有最大值-2.
解析:
解:(Ⅰ)f(x)=![]() sinx+
sinx+![]() .
.
故f(x)的周期为2kπ{k∈Z且k≠0}.
(Ⅱ)由π≤x≤![]() π,得
π,得![]() .
.
因为f(x)=![]() 在[
在[![]() ]上是减函数,在[
]上是减函数,在[![]() ]上是增函数.
]上是增函数.
故当x=![]() 时,f(x)有最小值-
时,f(x)有最小值-![]() ;而f(π)=-2,f(
;而f(π)=-2,f(![]() π)=-
π)=-![]() <-2,
<-2,
所以当x=π时,f(x)有最大值-2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 两问;理科全做.)
两问;理科全做.) 用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换.
用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换. I)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;
I)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;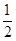 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: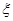 的分布列与期望
的分布列与期望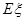 .
.