题目内容
已知f(x)=-x3+ax,其中a∈R.
(1)若f(x)在(0,1)上是增函数,求a的取值范围;
(2)若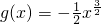 ,且f(x)<g(x)在(0,1]上恒成立,求a的取值范围.
,且f(x)<g(x)在(0,1]上恒成立,求a的取值范围.
解:(1)f'(x)=-3x2+a
∵f(x)在(0,1)上是增函数
∴f'(x)=-3x2+a≥0,对于x∈(0,1)恒成立
∴a≥3x2恒成立.
∴a≥3…(6分)
(2)∵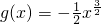 ,且f(x)<g(x)
,且f(x)<g(x)
∴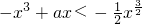 ,
,
∴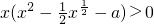 ,
,
∴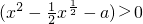 在(0,1)恒成立.…(8分)
在(0,1)恒成立.…(8分)
∴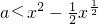 在(0,1)恒成立.
在(0,1)恒成立.
构造函数
则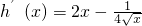
由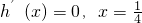 …(10分)
…(10分)
函数在 上单调减,在
上单调减,在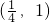 上单调增
上单调增
∴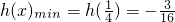
∴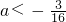 …(12分)
…(12分)
分析:(1)先求导函数,将f(x)在(0,1)上是增函数,转化为f'(x)=-3x2+a≥0,对于x∈(0,1)恒成立,分离参数可得a≥3x2恒成立,从而可求a的取值范围;
(2)根据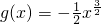 ,且f(x)<g(x),从而转化为
,且f(x)<g(x),从而转化为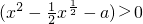 在(0,1)恒成立,分离参数可得
在(0,1)恒成立,分离参数可得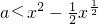 在(0,1)恒成立.构造函数
在(0,1)恒成立.构造函数 ,可知函数在
,可知函数在 上单调减,在
上单调减,在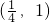 上单调增
上单调增
,从而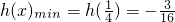 ,故求a的取值范围.
,故求a的取值范围.
点评:本题以函数为载体,考查函数恒成立问题,考查分离参数法求变量的取值范围,解题的关键是分离参数,利用求最值的方法,求参数的取值范围.
∵f(x)在(0,1)上是增函数
∴f'(x)=-3x2+a≥0,对于x∈(0,1)恒成立
∴a≥3x2恒成立.
∴a≥3…(6分)
(2)∵
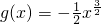 ,且f(x)<g(x)
,且f(x)<g(x)∴
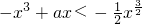 ,
,∴
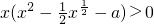 ,
,∴
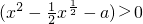 在(0,1)恒成立.…(8分)
在(0,1)恒成立.…(8分)∴
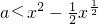 在(0,1)恒成立.
在(0,1)恒成立.构造函数

则
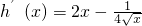
由
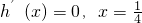 …(10分)
…(10分)函数在
 上单调减,在
上单调减,在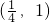 上单调增
上单调增∴
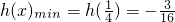
∴
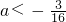 …(12分)
…(12分)分析:(1)先求导函数,将f(x)在(0,1)上是增函数,转化为f'(x)=-3x2+a≥0,对于x∈(0,1)恒成立,分离参数可得a≥3x2恒成立,从而可求a的取值范围;
(2)根据
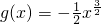 ,且f(x)<g(x),从而转化为
,且f(x)<g(x),从而转化为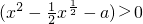 在(0,1)恒成立,分离参数可得
在(0,1)恒成立,分离参数可得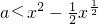 在(0,1)恒成立.构造函数
在(0,1)恒成立.构造函数 ,可知函数在
,可知函数在 上单调减,在
上单调减,在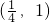 上单调增
上单调增,从而
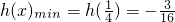 ,故求a的取值范围.
,故求a的取值范围.点评:本题以函数为载体,考查函数恒成立问题,考查分离参数法求变量的取值范围,解题的关键是分离参数,利用求最值的方法,求参数的取值范围.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目