题目内容
(选修4-4:坐标系与参数方程)已知曲线C的参数方程是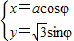 (φ为参数,a>0),直线l的参数方程是
(φ为参数,a>0),直线l的参数方程是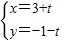 (t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.(Ⅰ)求曲线C普通方程;
(Ⅱ)若点
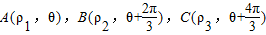 在曲线C上,求
在曲线C上,求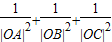 的值.
的值.
【答案】分析:(Ⅰ)消去直线l的参数t得普通方程,令y=0,得x的值,即求得直线与x轴的交点;消去曲线C的参数即得C的普通方程,再把上面求得的点代入此方程即可求出a的值;
(Ⅱ)把点A、B、C的极坐标化为直角坐标,代入曲线C的方程,可得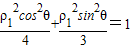 ,即
,即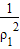 =
=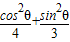 ,同理得出其它,代入即可得出答案.
,同理得出其它,代入即可得出答案.
解答:解:(Ⅰ)∵直线l的参数方程是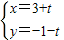 (t为参数),消去参数t得x+y=2,令y=0,得x=2.
(t为参数),消去参数t得x+y=2,令y=0,得x=2.
∵曲线C的参数方程是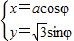 (φ为参数,a>0),消去参数φ得
(φ为参数,a>0),消去参数φ得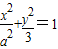 ,
,
把点(2,0)代入上述方程得a=2.
∴曲线C普通方程为 .
.
(Ⅱ)∵点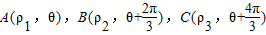 在曲线C上,即A(ρ1cosθ,ρ1sinθ),
在曲线C上,即A(ρ1cosθ,ρ1sinθ),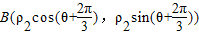 ,
,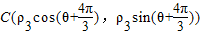 在曲线C上,
在曲线C上,
∴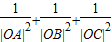 =
=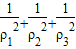 =
=

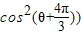
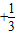
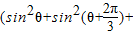
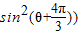
=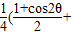
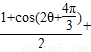
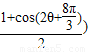
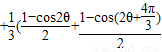
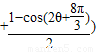
=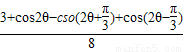 +
+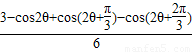
=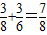 .
.
点评:正确消去参数化为普通方程、把极坐标化为直角坐标并代入曲线C的方程得出结论及熟练进行恒等变形是解题的关键.
(Ⅱ)把点A、B、C的极坐标化为直角坐标,代入曲线C的方程,可得
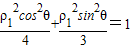 ,即
,即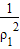 =
=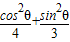 ,同理得出其它,代入即可得出答案.
,同理得出其它,代入即可得出答案.解答:解:(Ⅰ)∵直线l的参数方程是
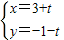 (t为参数),消去参数t得x+y=2,令y=0,得x=2.
(t为参数),消去参数t得x+y=2,令y=0,得x=2.∵曲线C的参数方程是
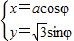 (φ为参数,a>0),消去参数φ得
(φ为参数,a>0),消去参数φ得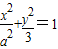 ,
,把点(2,0)代入上述方程得a=2.
∴曲线C普通方程为
 .
.(Ⅱ)∵点
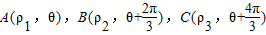 在曲线C上,即A(ρ1cosθ,ρ1sinθ),
在曲线C上,即A(ρ1cosθ,ρ1sinθ),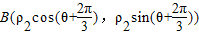 ,
,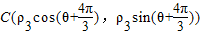 在曲线C上,
在曲线C上,∴
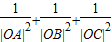 =
=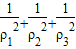 =
=

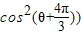
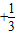
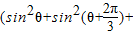
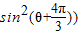
=
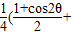
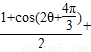
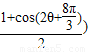
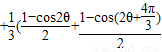
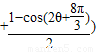
=
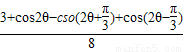 +
+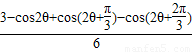
=
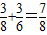 .
.点评:正确消去参数化为普通方程、把极坐标化为直角坐标并代入曲线C的方程得出结论及熟练进行恒等变形是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲