题目内容
已知函数f(x)=cos2x+1+ sin2x;求
sin2x;求
(1)函数f(x)的周期;
(2)函数f(x)的单调递减区间;
(3)函数f(x)在区间[0, ]上的最值.
]上的最值.
解: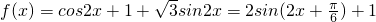 …(4分)
…(4分)
(1)最小正周期 ; …(6分)
; …(6分)
(2)当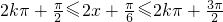 ,即
,即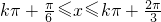 k∈Z时,函数f(x)单调递减,
k∈Z时,函数f(x)单调递减,
所以函数f(x)的单调递减区间为 .…(10分)
.…(10分)
(3)∵ ,∴
,∴ ,∴
,∴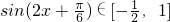
∴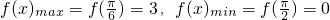 .…(14分)
.…(14分)
分析:由题设条件,先对函数f(x)化简,将其整理成f(x)=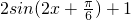
(1)由求周期公式求出周期,由于ω=2,周期易求;
(2)由正弦函数的性质,令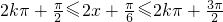 ,解出x的取值范围即得到函数的递减区间;
,解出x的取值范围即得到函数的递减区间;
(3)求函数f(x)在区间[0, ]上的最值,可先求出相位
]上的最值,可先求出相位 ,再求出
,再求出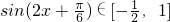 ,进而求出函数的最值.
,进而求出函数的最值.
点评:本题考查三角函数中的恒等变换应用,解题的关键是熟练掌握三角恒等变换公式,利用公式进行化简,熟练掌握正弦函数的性质也很关键,本题中考查了求函数在某个区间上的值域的方法,由内而外求出函数的取值范围,注意在解题时应用此方法,三角函数最值用此方法求解比用单调性求解简单不少.
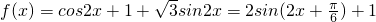 …(4分)
…(4分)(1)最小正周期
 ; …(6分)
; …(6分)(2)当
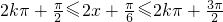 ,即
,即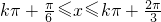 k∈Z时,函数f(x)单调递减,
k∈Z时,函数f(x)单调递减,所以函数f(x)的单调递减区间为
 .…(10分)
.…(10分)(3)∵
 ,∴
,∴ ,∴
,∴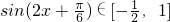
∴
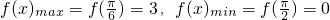 .…(14分)
.…(14分)分析:由题设条件,先对函数f(x)化简,将其整理成f(x)=
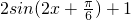
(1)由求周期公式求出周期,由于ω=2,周期易求;
(2)由正弦函数的性质,令
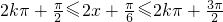 ,解出x的取值范围即得到函数的递减区间;
,解出x的取值范围即得到函数的递减区间;(3)求函数f(x)在区间[0,
 ]上的最值,可先求出相位
]上的最值,可先求出相位 ,再求出
,再求出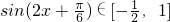 ,进而求出函数的最值.
,进而求出函数的最值.点评:本题考查三角函数中的恒等变换应用,解题的关键是熟练掌握三角恒等变换公式,利用公式进行化简,熟练掌握正弦函数的性质也很关键,本题中考查了求函数在某个区间上的值域的方法,由内而外求出函数的取值范围,注意在解题时应用此方法,三角函数最值用此方法求解比用单调性求解简单不少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )