Question

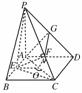
如图，在四棱锥P－ABCD中，PA⊥平面ABCD，四边形ABCD为正方形，PA＝AB＝4，G为PD中点，E点在AB上，平面PEC⊥平面PDC.

(1)求证：AG⊥平面PCD；

(2)求证：AG∥平面PEC；

(3)求点G到平面PEC的距离．

Answer 1

解：(1)证明：∵CD⊥AD，CD⊥PA，∴CD⊥平面PAD.

又AG⊂平面PAD，∴CD⊥AG.

又PD⊥AG，∴AG⊥平面PCD.

(2)证明：作EF⊥PC于F，

因面PEC⊥面PCD，∴EF⊥平面PCD.

又由(1)知AG⊥平面PCD，∴EF∥AG.

又AG⊄面PEC，EF⊂面PEC，

∴AG∥平面PEC.

(3)由AG∥平面PEC知A、G两点到平面PEC的距离相等，由(2)知A，E，F，G四点共面．

又AE∥CD，∴AE∥平面PCD.

∴AE∥GF.∴四边形AEFG为平行四边形，

∴AE＝GF.PA＝AB＝4，G为PD中点，FG綊CD，

∴FG＝2，∴AE＝FG＝2.

∴V_P－AEC＝(·2·4)·4＝.

又EF⊥PC，EF＝AG＝2，

∴S_△EPC＝PC·EF＝·4·2＝4.

又V_P－AEC＝V_A－PEC，∴S_△EPC·h＝，即4h＝16.

∴h＝.∴G点到平面PEC的距离为.