题目内容
(2013•淄博二模)若双曲线
-
=1(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则此双曲线的离心率为
.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
2
| ||
| 3 |
分析:依题意,可求得抛物线y2=2bx的焦点F(
,0),由
=
即可求得b,c之间的关系,从而可求得此双曲线的离心率.
| b |
| 2 |
| |FF1| |
| |F2F| |
| 5 |
| 3 |
解答:解:∵抛物线y2=2bx的焦点F(
,0),双曲线
-
=1(a>b>0)左、右焦点F1(-c,0),F2(c,0),
又线段F1F2被抛物线y2=2bx的焦点分成5:3两段,
∴
=
,即
=
,
∴c=2b;
又c2=a2+b2=4b2,
∴a2=3b2,
∴此双曲线的离心率e2=
=
=
,
∴e=
=
.
故答案为:
.
| b |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
又线段F1F2被抛物线y2=2bx的焦点分成5:3两段,
∴
| |FF1| |
| |F2F| |
| 5 |
| 3 |
| ||
c-
|
| 5 |
| 3 |
∴c=2b;
又c2=a2+b2=4b2,
∴a2=3b2,
∴此双曲线的离心率e2=
| c2 |
| a2 |
| 4b2 |
| 3b2 |
| 4 |
| 3 |
∴e=
| 2 | ||
|
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查双曲线的简单性质,由
=
即可求得b,c之间的关系是关键,考查分析与运算能力,属于中档题.
| |FF1| |
| |F2F| |
| 5 |
| 3 |

练习册系列答案
相关题目
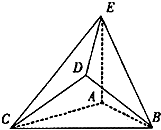 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=