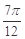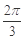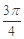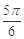题目内容
已知函数 的导函数为
的导函数为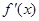 ,且满足关系式
,且满足关系式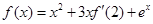 ,则
,则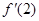 的值等于( )
的值等于( )
A.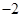 | B.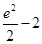 | C.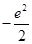 | D.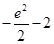 |
D
解析试题分析:∵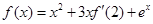 ,∴
,∴ ,令
,令 ,则
,则 ,即
,即 ,∴
,∴ ,故选D.
,故选D.
考点:导数的计算.

练习册系列答案
相关题目
下列求导运算正确的是( )
A.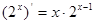 | B.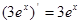 |
C.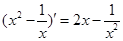 | D.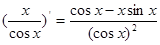 |
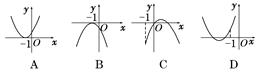
如图所示是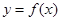 的导数
的导数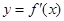 的图像,下列四个结论:
的图像,下列四个结论:
①  在区间
在区间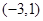 上是增函数;
上是增函数;
② 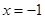 是
是 的极小值点;
的极小值点;
③  在区间
在区间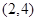 上是减函数,在区间
上是减函数,在区间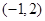 上是增函数;
上是增函数;
④ 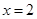 是
是 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是
| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
已知函数f(x)=ax2+3x-2在点(2,f(2))处的切线斜率为7,则实数a的值为( )
| A.-1 | B.1 | C.±1 | D.-2 |
设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当a<x<b时,有( )
| A.f(x)>g(x) |
| B.f(x)<g(x) |
| C.f(x)+g(a)>g(x)+f(a) |
| D.f(x)+g(b)>g(x)+f(b) |
设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,下面不等式在R上恒成立的是( )
| A.f(x)>0 | B.f(x)<0 |
| C.f(x)>x | D.f(x)<x |
已知函数f(x)=x(ln x-ax)有两个极值点,则实数a的取值范围是( ).
| A.(-∞,0) | B.(0,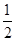 ) ) | C.(0,1) | D.(0,+∞) |
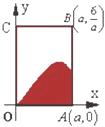
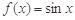 ,
,
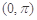 及直线x=a,
及直线x=a,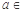
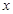 轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为 ,则
,则 的值是( )
的值是( )