题目内容
设各项均为正数的等比数列{an}中,a1+a3=10,a3+a5=40.设bn=log2an.
(1)求数列{bn}的通项公式;
(2)若c1=1, ,求证:cn<3.
,求证:cn<3.
(1)解:设数列{an}的公比为q(q>0),
由a1+a3=10,a3+a5=40,则 ,
,
∵a1≠0,②÷①得:q2=±2,又q>0,∴q=2.
把q=2代入①得,a1=2.
∴an= =2n,则bn=
=2n,则bn= =n;
=n;
(2)证明:∵c1=1<3,cn+1-cn= =
= ,
,
当n≥2时,cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1=1+ +
+ +…+
+…+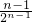 ③,
③,
∴ cn=
cn= +
+ +
+ +…+
+…+ ④,
④,
③-④得:
= =
= .
.
∴ <3(n≥2).
<3(n≥2).
故cn<3(n∈N*).
分析:(1)设出等比数列的公比,由已知条件列方程组求出等比数列的首项和公比,则等比数列{an}的通项公式可求,代入bn=log2an可求数列{bn}的通项公式;
(2)把求出的an和bn代入 ,把cn写成cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1,各项代入后利用错位相减法求cn,cn求出后即可得到结论.
,把cn写成cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1,各项代入后利用错位相减法求cn,cn求出后即可得到结论.
点评:本题考查了等比数列的通项公式,考查了数列的递推式,训练了利用错位相减法求数列的前n项和,属中档题.
由a1+a3=10,a3+a5=40,则
 ,
,∵a1≠0,②÷①得:q2=±2,又q>0,∴q=2.
把q=2代入①得,a1=2.
∴an=
 =2n,则bn=
=2n,则bn= =n;
=n;(2)证明:∵c1=1<3,cn+1-cn=
 =
= ,
,当n≥2时,cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1=1+
 +
+ +…+
+…+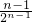 ③,
③,∴
 cn=
cn= +
+ +
+ +…+
+…+ ④,
④,③-④得:

=
 =
= .
.∴
 <3(n≥2).
<3(n≥2).故cn<3(n∈N*).
分析:(1)设出等比数列的公比,由已知条件列方程组求出等比数列的首项和公比,则等比数列{an}的通项公式可求,代入bn=log2an可求数列{bn}的通项公式;
(2)把求出的an和bn代入
 ,把cn写成cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1,各项代入后利用错位相减法求cn,cn求出后即可得到结论.
,把cn写成cn=(cn-cn-1)+(cn-1-cn-2)+…+(c2-c1)+c1,各项代入后利用错位相减法求cn,cn求出后即可得到结论.点评:本题考查了等比数列的通项公式,考查了数列的递推式,训练了利用错位相减法求数列的前n项和,属中档题.

练习册系列答案
相关题目
 是各项均为正数的等比列数列,
是各项均为正数的等比列数列, ,若
,若 ,
, ,求
,求 .
. 是各项均为正数的等比列数列,
是各项均为正数的等比列数列, ,若
,若 ,
, ,求
,求 .
. ,若数列{bn}是单调递增数列,求实数λ的取值范围.
,若数列{bn}是单调递增数列,求实数λ的取值范围.