题目内容
用总长为14.8米的钢条制成一个长方体容器的框架,如果所制的容器的底面的长比宽多0.5米,那么高为多少时容器的容器最大?并求出它的最大容积.
解:设容器底面宽为xm,则长为(x+0.5)m,高为(3.2-2x)m.
由 解得0<x<1.6,
解得0<x<1.6,
设容器的容积为ym3,则有
y=x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x(0<x<1.6) y′=-6x2+4.4x+1.6, 令y′=0,即-6x2+4.4x+1.6=0,
解得x=1,或x=-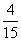 (舍去).
(舍去).
∵0<x<1时,y′>0;1<x<1.6时,y′<0.
∴在定义域(0,1.6)内x=1是唯一的极值点,且是极大值点,
∴当x=1时,y取得最大值为1.8.
此时容器的高为3.2-2=1.2m.
答:容器高为1.2m时容器的容积最大,最大容积为1.8m3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的顶点在原点,始边与
的顶点在原点,始边与 轴的非负半轴重合,终边经过点
轴的非负半轴重合,终边经过点 。
。 的值;(2)求
的值;(2)求 。
。 的单调递增区为 .
的单调递增区为 .  ,
, 的法向量分别是
的法向量分别是 ,
, ,若
,若 ,则
,则 的值( )
的值( ) 为空间的一个基底,且
为空间的一个基底,且 ,
, ,
, ,能否以
,能否以 作为空间的一个基底 (填“能”或“不能”).
作为空间的一个基底 (填“能”或“不能”).  ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 、
、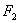 分别是双曲线
分别是双曲线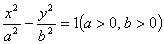
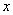 轴的直线与双曲线交于A,B两点,若△
轴的直线与双曲线交于A,B两点,若△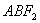 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )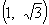 B.
B.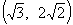 C.
C.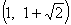 D.
D.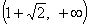
 的终边与单位圆交于点
的终边与单位圆交于点 ,且
,且 那么
那么 的值是( )
的值是( ) B.
B.  C.
C. D.
D.
 ,
, ,则
,则 中元素的个数为
中元素的个数为