Question

已知椭圆C₁的方程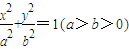为，离心率为，两个焦点分别为F₁和F₂，椭圆C₁上一点到F₁和F₂的距离之和为12，椭圆C₂的方程为，圆C₃：x²+y²+2kx-4y-21=0（k∈R）的圆心为点A_k．
（I）求椭圆C₁的方程；
（II）求△A_kF₁F₂的面积；
（III）若点P为椭圆C₂上的动点，点M为过点P且垂直于x轴的直线上的点，（e为椭圆C₂的离心率），求点M的轨迹．

Answer 1

【答案】分析：（I）设椭圆C₁的半焦距为c，利用离心率，椭圆C₁上一点到F₁和F₂的距离之和为12，椭圆定义，求出a，b，然后求椭圆C₁的方程；
（II）求出点A_k的坐标，直接求△A_kF₁F₂的面积；
（III）椭圆C₂的方程为，设M（x，y），P（x，y₁），其中x∈[-4，4]．
求出，化简16（x²+y₁²）=9（x²+y²）．由点P在椭圆C上得，
求出点M的轨迹方程为，轨迹是两条平行于x轴的线段．
解答：解：（I）设椭圆C₁的半焦距为c，
则 2a=12

解得a=6，c=3，（3分）
于是b²=a²-c²=36-27=9，（4分）
因此所求椭圆C₁的方程为：（5分）
（II）点A_k的坐标为（-k，2），
则．（10分）
（III）椭圆C₂的方程为，
设M（x，y），P（x，y₁），其中x∈[-4，4]．
由已知得，
而e=，故16（x²+y₁²）=9（x²+y²）．
由点P在椭圆C上得，
化整理得9y²=112，（13分）
因此点M的轨迹方程为，（14分）
轨迹是两条平行于x轴的线段．（15分）
点评：本题考查椭圆的应用，考查分析问题解决问题的能力，计算能力，逻辑思维能力，是中档题．