题目内容
已知椭圆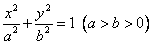 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B,
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B,
(Ⅰ)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e;
(ⅱ)若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围;
(Ⅱ)设直线AB与x轴、y轴分别交于点M,N,求证: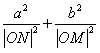 为定值。
为定值。
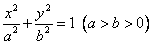 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B,
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B, (Ⅰ)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e;
(ⅱ)若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围;
(Ⅱ)设直线AB与x轴、y轴分别交于点M,N,求证:
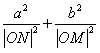 为定值。
为定值。 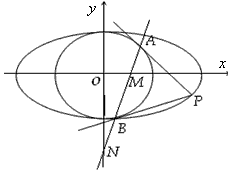
解:(Ⅰ)(ⅰ)∵圆O过椭圆的焦点,圆O:x2+y2=b2,
∴b=c,
∴ ,
,
∴ ,
,
∴ ;
;
(ⅱ)由∠APB=90°及圆的性质,可得 ,
,
∴ ,
,
∴ ,
,
∴ ;
;
(Ⅱ)设 ,则
,则 ,
,
整理得 ,
,
 ,
,
∴PA方程为: ,
,
PB方程为: ,
,
∴ ,
,
∴ ,
,
直线AB方程为 ,
,
令x=0,得 ,令y=0,得
,令y=0,得 ,
,
∴ ,
,
∴ 为定值,定值是
为定值,定值是 。
。
∴b=c,
∴
 ,
, ∴
 ,
, ∴
 ;
; (ⅱ)由∠APB=90°及圆的性质,可得
 ,
, ∴
 ,
, ∴
 ,
, ∴
 ;
;(Ⅱ)设
 ,则
,则 ,
,整理得
 ,
, ,
, ∴PA方程为:
 ,
,PB方程为:
 ,
, ∴
 ,
, ∴
 ,
,直线AB方程为
 ,
,令x=0,得
 ,令y=0,得
,令y=0,得 ,
, ∴
 ,
, ∴
 为定值,定值是
为定值,定值是 。
。
练习册系列答案
相关题目
 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 为定值.
为定值.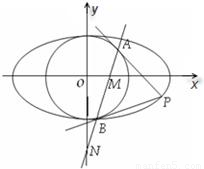
 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 为定值.
为定值.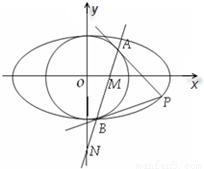
 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 为定值.
为定值.
 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 为定值.
为定值.
 和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 为定值.
为定值.